Управління запасами

Управління запасами

Оптимальний розмір запасів

Для отримання більшого прибутку необхідно звести змінні витрати до мінімуму. Тут ви розглянете проблему мінімізації змінних витрат за допомогою управління запасами.

Нехай на протязі місяця ви продаєте q одиниць продукції , котру ви закупаєтє n разів по Q одиниць в партії. При цьому витрати на зберігання однієї штуки на місяць становлять , а вартість заказа партії дорівнює f .

Тоді сумарні витрати підтримки запасів дорівнюють:

(1.66)

Змінні витрати (VC)=витрати на зберіганняштук на протязі місяця + Вартість заказа nартій . У формулі (1.66) стоїть вартість зберігання штук на протязі місяця, так як по ходу продаж , кількість зберігаємого товару буде поступово зменьшуватись до 0 ,після чого буде закупатися нова партія (мал(1.24)).

Знайдемо мінімум змінних витрат VC

.

Теорема 1.7. Об оптимальному розмірі закупаємої партії:

Нехай в одиницю часу ,наприклад ,місяць, Ви закупаєте q одиниць продукції, котру ви закупаєтє n разів по Q одиниць в партії. При цьому витрати на зберігання однієї штуки на місяць становлять , а вартість заказа партії дорівнює f .

Тоді оптимальна кількість заказів визначається за формулою:

(1.67)

Оптимальний розмір закупаємої партії визначається формулою:

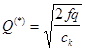(1.68)

Оптимальні змінні витрати підтримки запасів визначаються формулою:

(1.69)

Доведення теореми (1.7):

Для цього візьмемо похідну по Q та прирівняємо її до 0:

або

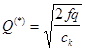
Формула (1.68) дає оптимальний розмір закупаємої партії ,при цьому кількість закупок буде визначатися за формулою:

або

,

а оптимальне змінні витрати підтримки запасів визначаються за формулою:

або

Теорема доказана.

Так, якщо на протязі місяця Вам треба 1000 штук,q=1000,вартість заказа партії 10$ , При цьому витрати на зберігання однієї штуки на місяць становлять $1.5, формула (1.69) для визначення кількості штук дає:

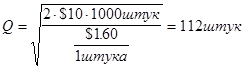
формула (1,67)-кількість закупок на місяць:

формула (1,69)-мінімально можливі витрати на підтримку запасів:

в місяць

при наівному рішенні купити відразу 1000 одиниць Ви би мали:

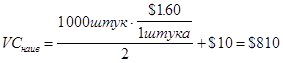
порівняно з «наівним» рішенням ви зекономили

$810-$179.85=$630.15

Таким чином раціональне управління запасом дозволило зменшити витрати зберігання у

Чисельний приклад 1,28

Нехай у вас витрати зберігання дорівнюють $1.6/штука за місяць ,на місяць потрібно 1000 штук, вартість заказа партії $10. Вас цікавлять витрати на підтримку запасів в залежності від об’єму закупаємої партії

В першій строке розміщені різні значення об’єму закупаємої партії в другій витрати на збереження запасів.

Кількість зберегаємих на складі деталей показано на малюнку 1,25.

Визначення 1,37

Коефіцієнт економії КЕ

Коефіцієнт економії КЕ є відношення витрат початкового, нівного варіанта закупки відразу q одиниць товару до витрат оптимального варіанту.

Визначення 1,38 Рівень оптимальних витрат РОВ

Визначимо рівень оптимальних витрат РОВ як відношення витрат оптимального варіанта до витрат наівного варіанта .

Коефіцієнт економії КЕ показує в скільки раз ви знизили витрати , а рівень оптимальних витрат РОВ показує долю оптимальних витрат від витрат початкового варіанту.

Теорема 1,8 Коефіцієнт економії та Рівень оптимальних витрат

При виконанні умов теореми 1,7 вірно:

(1,70)

,де (1,71)

(1,72)

Доведення:

Рівень оптимальних витрат визначається за формулою:

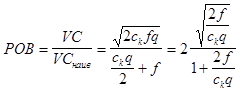
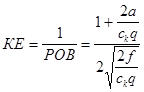
Замінивши на х отримаємо:

Теорему доведено.

Знайдемо похідну КЕ по х :

Таким чином КЕ мінімален та дорівнює одиниці при x=1, або в цьому нема нічого не звичайного :в цьому випадку розмір оптимальної партії дорівнює q та ви робите лише одну покупку, як в наівному варіанті.

Чисельний приклад 1,29 Коефіцієнт економії

Коефіцієнт економії та рівень оптимальних витрат залежать від коефіцієнта х,

Нас цікавлять значення коефіцієнта економії та рівня оптимальних витратв залежності від значення х ,розрахунки робимо за формулами (1,70) (1,71).

В першій строчці знаходиться параметр х ,розрахований по формулі(1,72),в другій та третій коефіцієнти РОВ та КЕ ,розраховані по формулі (1.70)та(1.71)

Оптимальний розмір готівки

Нехай тепер Вам на місяць треба готівки в розмірі М. Інші вільні кошти ви тримаєте в банку або в цінних паперах, наприклад облігаціях, приносящих r% на місяць(в одиничний проміжок часу).Кожного разу при знятті коштів з банківського депозиту або при продажу облігацій Ви платите фіксовану суму за проведення операцій в розмірі f наприклад комісійні за продаж облігацій Вам треба визначити оптимальний режим взяття готівки.

Ця задача аналогічна попередній задачі визначення оптимального розміра запасів. Розгляньте її більш детально. Якщо ви будете знімати кошти партіями розміром m , то в середньому у Вас на руках будеготівки: m в момент зняття грошей та 0 перед зняттям. Тому ви не до отримаєте відсотки розмірі . В тій же час ( період) Ви будете брати гріши раз, виплачуючи за це комісійні в розмірі .Тому сумарні витрати

VC

зберігання готівки будуть: (1,73)

Вас цікавить мінімізація цих витрат .Для цього візьмемо похідну по m та прирівняємо її до 0 :

(1,74)

Ви бачите ,що формула(1,74) повністю співпадає з формулою (1.68).

Так, якщо на місяць вам потрібно $10 000,гроши ви тримаєте в банку на рахунку з 6% річних або 0,5%на місяць та витрати знаття грошей становлять $2, наприклад , комісійні за зняття грошей за допомогою пластикової картки ,та по формулі (1.74) Ви знаходите оптимальний розмір суми для зняття:

Ви бачите, що оптимальні суми зняття грошей становлять близько $2800

Якщо ж гроши лежать на депозиті під 12% річних або 1% річних ,то оптимальний розмір знімаємої суми становлять вже

1.6.3 Довжина черги та оптимальний розмір запасів

В попередньому розділі ви розглянули управління оборотним капіталом в умовах визначеності .Але ж якщо до вас приходять покупці випадковим чином та закупають випадкову кількість товару, то не маючи запасу, ви не завжди будете в змозі задовольнити бажання покупців ,що може привести чи до сплати неустойки за не можливість доставити партію товару , чи до втрати покупців. В тей же самий час мати дуже великий розмір запасу є невигідним з за заморожених в запасах коштів та з за плати за зберігання запасів.

Розгляньте цю ситуацію більш детально. Нехай до вас в одиницю часу з ймовірністю х приходить запит на одиничну партію товару ,та з ймовірністю y обслуговується запит на одиничну партію товару. Вас цікавить середня величина незадоволеного попиту, котрий у Вас накопиться з часом.

Теорема 1.9 Середня довжина черги

Нехай довжина черги може приймати цілі невід’ємні числа :0,1,2,.... При цьому равна 0 довжина черги означає відсутність черги. Нехай до вас в одиницю часу з ймовірністю х приходить запит на одиничну партію товару ,та з ймовірністю y обслуговується запит на одиничну партію товару, з ймовірністю 1-х-у довжина черги залишається не змінною.

Тоді середня довжина черги визначається за формулою

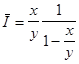(1,75)

Доведення:

Нехай r(i) визначає ймовірність того, що Ви маєте незадоволений попит в І партій Тоді ймовірність того, що в наступний момент часу з’явиться новий клієнт та середня величина незадоволеного попиту стане І+1 з ймовірністю xr(I):

(1,76)

де ймовірність переходу з стану з величиною незадоволеного попиту І до стану з величиною незадоволеного попиту І+1.

З ймовірністю у Вам підвезуть одиничну партію товару та середня величина незадоволеного попиту стане І-1 з ймовірністю :

(1,77)

З ймовірністю 1-х-у нічого не трапиться :ні з’явиться новий клієнт, ні підвезуть

нову партію Тому ймовірність того що довжина черги залишиться рівною І дорівнює :

(1,78)

Якщо в даний момент часу ви не маєте незадоволеного попиту (ймовірність відсутності незадоволеного попиту дорівнює r(0) , то можливі дві ситуації: з’явлення нового покупця з ймовірністю х ,та відсутність змін з ймовірністю (1-х):

(1,79)(1,80)

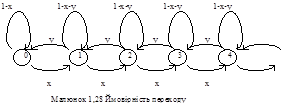
З за малості х у (цього можна добитися зменшуючи величину часового проміжку до 0 )Ви нехтуєте можливістю того, що одночасно трапиться декілька подій , наприклад одночасно прийдуть декілька покупців. Ви шукаєте середню величину, тобто стаціонарний стан системи (1,76-1,80) В цьому випадку рівняння ви можете написати:

(1,81)(1,82)

Рівняння (1.81)(1.82) мають розв’язок:

В більш компактному вигляді:

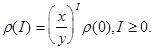
Тепер вам залишилось отримати чисельні значення для ймовірності r(I),І0. Для цього випишемо рівняння нормування: ймовірністю 1 система буде мати задовільнений попит чи яку небуть величину незадоволеного попиту . Математично ця умова запишеться у вигляді:

або

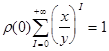
Маючи вираз для суми геометричної прогресії:

Ви отримаєте :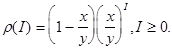

Найдемо середню довжину черги :

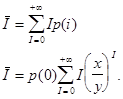
Тепер вам залишилось підрахувати ряд :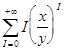

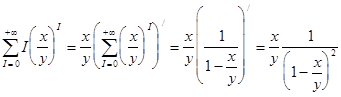
Таким чином ми отримали:

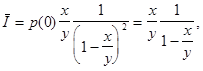
Теорему доведено.

Чисельний приклад 1,30 Довжина черги.

Вас цікавить довжина черги в залежності від відношення х/у- ймовірності отримання нового замовлення до ймовірності обслуговування присутнього замовлення в одиницю часу.

Довжина черги:

В першій строчці розташовані різні відношення х/у ,в другій Відповідні очікувані довжини черги І розраховані за формулою (1,75) Ви бачите що для мінімальної довжини черги ймовірність(швидкість) обслуговування клієнта повинна перевищувати ймовірність(швидкість) приходу клієнтів. Так на приклад для середньої довжини черги в 2 особи таке перебільшення повинно складати 33%

Теорема 1,10 Оптимальна величина запасу

Нехай неустойка за незадовільненя попиту дорівнює М, вартість зберігання однієї одиниці товару є , ймовірність приходу клієнта в одиницю часу є х, ймовірність задоволення клієнта в одиницю часу є у.

Тоді оптимальний розмір запасу L визначається за формулою:

(1,83)

Доведення:

Ймовірність r(I>L) того, що величина незадоволеного попиту буде більша за L розраховується за формулою: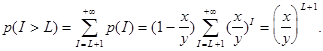

тому середня величина запасу для задоволення усіх покупців повинна дорівнювати або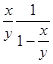

Якщо при не можливості задовольнити попит , ви платите неустойку в розмірі М, то для визначення оптимальної величини запасу L, Ви розв’язуєте задачу:

(1,84)

Де - вартість зберігання 1 одиниці товару.

Задача(1.84) розв’язується аналітично, але її можна розв’язати чисельно або графічно. Оптимальна величина резервного запасу L задовольняє умові:

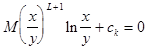
або

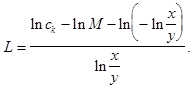
Теорему доведено

Так при витратах зберігання $1.6/штука,=0,25,М=$100 ви отримаєте значення оптимального резервного запасу

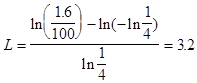
або 3-4 штуки. Якщо неустойка зросте до $1000 то оптимальний запас збільшится до 5 штук. Якщо ж =0,8 то оптимальні величини резервного запасу будуть вже 6,7 та 17 штук відповідно для штрафу $100 та $1000.

Чисельний приклад1,31 Оптимальна величина резервного запасу прирізних відношеннях витрати зберігання однієї одиниці до величини неустойки та відношення ймовірності приходу клієнта до ймовірності обслуговування клієнта.

В першій строчці розташовані різні відношення ,в першому стовпці в таблиці оптимальна величина резервного запасу розраховується по формулі (1.83)

• Питання ціноутворення
• Диференціювання ціни
• Використання знижок для маркетингового аналізу покупців

Інші статті по менеджменту

Кризове явище функціонування та розвитку організації
Дати визначення наступним термінам Предмет курсу "Антикризове управління" –– проблеми та можливі і реальні фактори кризових явищ, тобто всі прояви загострення протиріч, які ...

Імідж ділової людини та організації
Англійське слово „імідж" означає не що інше, як „образ". Імідж - це штучне створення неперевершеного образу. Зайве переконувати, наскільки важливим для секретаря-референта ...

Методи прийняття управлінських рішень
Діяльність будь-якого керівника пов'язана з розробкою і реалізацією рішень у рамках виконання їм посадових обов'язків у компанії. Основний принцип управління - єдиноначальність. Суть йог ...